How was the number π first discovered?

Unfortunately, the use of the number π is older than recorded history so… who knows?  But the use of number π at the beginning of recorded history wasn’t too sophisticated, so we can make guesses.

π is the ratio of a circle’s circumference to its diameter.  Everything about π boils down to that definition.

That the distance across a fixed shape is proportional to the distance around it is nothing special.  The same is true for absolutely every shape.  If you double the size of any shape, both the distance across and around with double as well, so their ratio stays the same.

Measure the distance around and across any square, then divide, and you’ve got 4.

Knowledge of the fact that the ratio of the circumference to the diameter of circles is some particular fixed number is older than recorded history.  The fact that the ratio isn’t exactly three takes a little care and precision.  Figuring out that the ratio has an infinite and non-repeating decimal expansion (that starts with 3.14159265358979323846264…) takes a little math and time.

A Babylonian tablet from around 4,000 years ago that declares the value of π to be 3.  Could be worse.

If you can nail one end of a piece of string down and tie a quill or piece of charcoal to the other, then you can draw a damn-near-perfect circle.  With a longer piece of string (at least 2π times as long, in fact) and a ruler, you can measure the circumference and as long as you’re careful, it’s pretty obvious that number π≠3.  As long as the error in your measurements is below 4%, you can tell the difference.  The Babylonians created the Code of Hammurabi and some pretty impressive buildings, so presumably, they could create a meter stick with centimeter marks (or rather, a kuš stick with šu-si marks).  It turns out the tablet in the picture above is really a “cheat sheet” for roughly approximating the area of circles.  They were known to have used, an approximation within half a percent of the correct value.  Which, for the bronze age, is fine.

Since π shows up practically anytime you’re doing math involving circles, there was a heck of a lot of opportunities for people in the ancient world to notice it and we can’t be sure which first caught their eye (this is the drawback of discoveries that are older than history).  For example, the volume, v, of a barrel with height h and diameter d is.  If you want to predict how much water a cylindrical barrel can hold to within a couple percent, then you need to know π to at least a couple digits.

All of this is to say that number π, while full of mathematical mysteries or whatever, is not some abstract idea.  It’s something you can physically measure.  Well… you can tell it’s not three anyway.  The larger the circle and the better your measurements, the more digits of number π you can discover, but the law of diminishing returns kicks in faster than an all-you-can-eat-week-old-sushi buffet.

By the time you know number π out to N digits, you know the ratio of the circumference to the diameter of a circle to on the order of 1 part in 10^N.  For example, if you know that number π≈3.14, then you can fit a bike tire onto a rim to within a cm.  If you know that π≈3.1415, you can build a fence around a circular acre to within a cm.  And if you know that π≈3.1415926535, you can wrap a cable around the Earth with less than a cm of wasted cable.  Arguably, knowing π out to ten or more digits is aggressively pointless, but that has never stopped mathematicians from practicing their cruel craft.  Not once.

The definition of π not only gives us a recipe for physically measuring it, but also hundreds of ways to mathematically derive it, and that’s where the real precision comes from.  Mathematicians like Archimedes and Liu Hui, and some nameless Egyptian a couple millennia before them, were able to approximate π using polygons.  Liu Hui calculated number π accurately out to three digits, a record slightly better than Archimedes’, that held for about a thousand years.  Which is strange.

During the Roman siege of Syracuse, general Marcellus ordered that Archimedes should be captured alive because clever knows no nation.  Unfortunately, geometry-ing to the very end, Archimedes was a jerk to the very first Roman he met.

Either Archimedes and/or historians really dropped the ball, or people in ancient Greece were more level-headed about knowing lots of digits of π than we are today.  For a given circle, the points on an “inscribed polygon” touch the circle (so it’s inside) and the middle of the edges of a “circumscribed polygon” touch the circle as well (so it’s outside).  Archie approximated π by inscribing and circumscribing 96-gons in and around the circle and calculating their perimeters.  An inscribed polygon gives a lower bound, and a circumscribed polygon gives an upper bound, for the value of π.

But here’s the thing: Archie didn’t just find the perimeter of 96-gons, he invented an iterative algorithm to calculate the perimeter of 2n-gons given n-gons.  That is, he started with hexagons (6-gons) and bootstrapped up to 12-gons, 24-gons, 48-gons, and then inexplicably stopped at 96-gons.  Evidently, he had better things to do than calculate more digits of π.  Which, to be fair, is not a high bar.  He may have just declared the problem solved, since anyone following his procedure could find as many digits as they’d want, and moved on to heat rays or something (seriously, dude tried to build a solar heat ray to defend Syracuse).

Every time Archimedes’ iterative algorithm has used the estimate for π gets about 4 times better (its rate of convergence is 1/4).  Which is less impressive than it sounds; that’s about 3 decimal digits every 5 iterations.  Archie used it 4 times to go from hexagons to enneacontahexagons for an accuracy of about 3 decimal places.  If he had bothered to repeat the process, say, ten more times, he would have known the first 9 decimal digits.  Definitely not useful, but potentially brag-worthy.

Modern algorithms put those old approximations to shame instantly.  Archimedes’ technique converges linearly to the true value of π (you gain about the same number of digits every time you use the algorithm).  Things didn’t really start to pick up until we invented quadratically converging algorithms, which double the number of known digits with each iteration.  That is: if you know ten, then after the next iteration, you’ll know twenty.  The fastest algorithms today converge nonically (the accurate decimal expansion gets nine times longer with each step).

The definition of π, the ratio of the circumference to the diameter of a circle, allows us to measure it directly, but inaccurately, or calculate it precisely, but pointlessly.  The more abstract properties of π, like going on forever without repeating (which it does) or containing every possible pattern (which it might), require more than brute force discovery of digits.  These more abstract properties are based on the definition of π, not its value, and can typically be proven or disproven without knowing even a single digit.  Math is useful in the physical world, but it doesn’t “live here”.  Number π has physical significance, but we use its mathematical properties to learn about it.

---

Answer Gravy: Ancient people were very clever and when they lived long enough they even got to prove it.  This gravy is the math behind Archimedes’ algorithm.  This isn’t exactly the way he wrote it.  Ancient Greek mathematicians suffered from the demonstrably false belief that a minimum of words is the secret to a maximum of understanding.  So, even translated, their proofs still read like Greek.


Mr. Medes’ method was this.  If I_n is the perimeter of the inscribed polygon and C_n is the perimeter of the outer n-gon, then:



You could rigorously prove that as you increase the number of sides the perimeters will get closer to number π (the circumference of the circle) using lots of equations or something, or you can just draw a picture and say “look… they clearly do”.

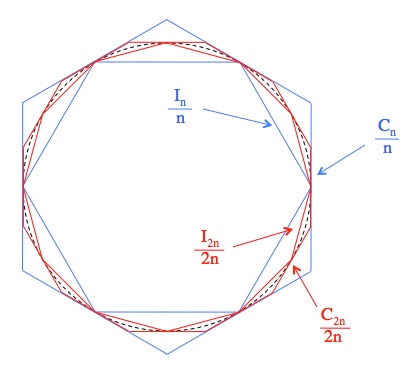
A circle (dashed line) with its inscribed and circumscribed n-gons (blue) and 2n-gons (red).  The length of each segment is the total perimeter divided by the number of segments (hence all the dividing by n’s).

If you stick six triangles together, you get a hexagon and with a little trigonometry, you find that if your circle has a diameter of 1, then the inscribed hexagon’s perimeter is I₆ = 3 and the circumscribed hexagon’s perimeter is C₆ = 2√3 ≈ 3.46.

To find the perimeters for dodecagons, plug C₆ and I₆ into the iterative equations:

 

These perimeters are both closer to number π than those before the iteration and since  for all n, this gives us an ever-diminishing range where π can be found.  Here’s why it works:

In/circum-scribing n-gons on a circle produces some useful symmetries.  In particular, it allows us to draw some triangles and rapidly figure out their angles.

One of the sides from an inscribed n-gon and a corner from a circumscribed n-gon.  The lines inside are from the new 2n-gons.  The red shaded triangles are similar to each other (have the same angles) and the blue outlined triangles are similar.

A full circle is 360 degrees, so each side of an n-gon spans 360/n degrees.  In this case, a is half of one of those angles, so a=180/n.

Both B's are complementary to a (they sum to 90), since the sum of angles in a triangle is 180 and the third angle is 90 (asymmetry we get from the fact that radial lines always hit a circle at a right angle).  So, b = 90-180/n.

c and b are complementary, so c = a = 180/n.

c+d = 180, so d = 180-c = 180-180/n.

The sum of angles in a triangle is 180, so d+e+e = 180 and e = 90-d/2 = 90/n.

Finally, b+e+f = 90, so f = 90-b-e = 90/n.

Since f=e, the two red triangles have the same angles: they’re “similar triangles“.  Similarly, since c=a the two blue triangles have the same angles and are also similar.  When two triangles are similar, the ratios of their sides are the same.



Using the similarities on the blue triangles we can say:



and of course, using the red triangles:



So, starting with a little geometry and the definition of π we can construct a bootstrapping method for approximating it better the longer we bother to work at it.

Multiplication and long division can be done by hand pretty easily.  The hardest part of this iterative algorithm facing any ancient person is the square root.  Also making the scratch paper.  Fortunately, there are tricks for that too.  For example, if you want to take the square root of S, just make a guess, x, then calculate and what you get will be a number closer to than your original guess, x.  This method was known to the Babylonians and Archimedes (it is, in fact, “the Babylonian method”) and it converges quadratically, so it achieves whatever (reasonable) accuracy you’re hoping for almost instantly.

The point here is that you can, through the injudicious use of reason, time, and scratch paper alone, find number π to as many digits as you would ever need.

You can read a little more about the Babylonian tablet here.